前言

交大的 sakura 最近开了，真的好看死我了。不过不幸的是本人近来牙齿不适，常受牙医电钻酷刑，今天下午的樱花诗会便因为需要去龈下刮治咕掉了。

扯远了，这篇主要是总结一下我们班数据结构课的近两次小作业的有关知识点。第一次比较懒没有做B班题，所以只提到A班的那部分题。

本篇文章对没学过相关知识的读者不太友好，主要用作自己巩固知识用。所有题目均为ACM班班内OJ上对应题号的题目。

---

P1088 春樱对决

题意

\(1 - N\) 这 \(N\) 个数按顺序排成一列，一次删除操作定义为：

从当前起点开始向右数（起点为第1个点），如果遇到边界点就反向继续数，直到遇到第 \(M\) 个点，删除它（即今后数数时不再考虑），并把下一次操作起点定为它的下一个点（同样，下一个点也遵循边界反弹）。

给定 \(N,M\)，请问删除 \(N-1\) 次后最后剩下的点编号为？\(N \le 10^5,\ M \le 10^9\)。

解法

最朴素的想法：模拟，链表删除 O(1)，但是数 M 个得跳 O(N) 次（为什么是 N ？因为可以根据跳的周期性将 M 的范围缩小），数组删除 O(N)。

自然想到用块链优化，然后直接过了。复杂度 \(O(N \sqrt N)\)

---

P1089 聚餐

题意

有 \(M\) 组要求，每组要求由若干个绝对值为 \(1-N\) ，可正可负的数构成。

一个选择为 \(1-N\) 的一个子序列。一个选择满足一个要求定义为：存在该要求中的一个数，若该数为正，则选择中含该数；若该数为负，则选择中不含该数。

给定要求，问是否存在满足所有要求的选择？\(N\le20,\ M\le60\)。

解法

居然可以直接暴力，一个选择压成 \(2^{20}\) 的数，枚举所有选择判断是否满足条件。复杂度 \(O(2^NM)\)。

---

P1090 Bang

题意

给定连通无向图 \(G(N,M)\)，每个点都有一个点权。有两种操作：

1. 修改某个点的点权。
2. 给定两个人的起点 \(S_1,S_2\)，之后这两个人可以在图上游走但要走必须同时走，步数没有限制。问走若干步后两人所在地点权差绝对值的最小值。

\(N \le 10^5, M \le 2 \times 10^5, Q \le 10^5\)。

解法

两个人同时走是很关键的性质，可以自己手玩一会儿。

我们当然是想让他们走到同一个点的，这当且仅当起点间存在奇数长度（这里，长度定义为路径上的点数）路径才能做到。因此如果存在奇环，一定能走到。

想到奇环自然会想到黑白染色。我们发现为什么会永远走不到呢？是因为若此图能黑白染色，那两个人一定只能在不同颜色上走。由于可以走任意步，实际上就是问所有黑点和所有白点间点权差最小的两个点是多少，动态维护这个。

平衡树可以解决，当时做的时候是平衡树+优先队列，每次改点相当于删一个点、插一个点。复杂度 \(O(N \log N)\)。

---

P1094 Pyramid

题意

给定 \(N\) 行 \(M\) 列网格，每个格子都有一个权值。求如下子图形覆盖的最小权值和（指该图形所占网格的所有权值和）：

一个 \(b\) 行 \(a\) 列的矩形，从中挖掉一个 \(d\) 行 \(c\) 列的矩形。挖掉的格子不能在\(b\) 行 \(a\) 列的矩形的边界上。如下图灰色部分。

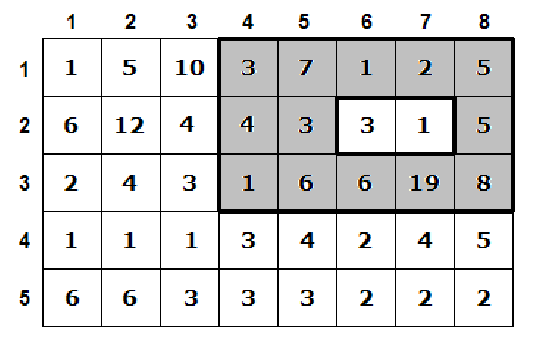
\(3\le N, M \le 1000\)。

解法

二维线段树暴过！\(O(N \log^2 N)\)

---

P1095 推箱子

题意

给定一个只有一个箱子的推箱子网格地图，问最少推几次箱子能到目的地？

形式化地，有一个 \(N \times M\) 网格地图，地图上有四种状态：

1. 玩家，可以上下左右移动
2. 箱子，如果对应方向无障碍物可以被玩家推动
3. 障碍，玩家和箱子均不可通过
4. 空格，玩家和箱子均可通过

给定玩家、箱子的起始位置，问最少要推几步能把箱子推到目的地？注意这里问的是箱子移动步数，人空走是不算的。\(N,M \le 100\)。

解法

鉴于我们不关心人自己走，所以我们发现人只需干两件事：推箱子和走到箱子的另一个方向。因此只要记状态：\(f(i,j,dir)\) 表示箱子位置为 \((i,j)\)，人在箱子的 \(dir\) 方向。

转移就两种：推和人到别的方向。最坏复杂度 \(O((NM)^2)\) 。

---

P1093 排方阵

题意

给定 \(N\) 行 \(M\) 列网格，每个格子都有一个权值。求一个使得其中权值最大值和最小值之差最小的 \(a \times a\) 子正方形。\(N,M \le 1000\)。

解法

静态二维RMQ，可以二维ST表，不过鉴于我懒还是直接二维线段树了。

---

P1098 排队

题意

给定长度为 \(N\) 的序列，问满足以下条件的最长连续子序列：

子序列首项为该子序列最小值，末项为最大值，且中间项均不等于首尾项。\(N \le 5 \times 10^5\)。

解法

靠，这题一开始就想出来了，后来以为正确性错了。

考虑某一个数结尾的符合条件的序列最多有多长，

首先要保证该数是序列最大值，于是即为一直往左延伸直到遇到第一个大等于自己的数。然后又要保证左端点是最小值，因此直接在这个范围查区间最小值即可，注意有个不能相同的条件，所以如果有多个最小值要判一下。

“往左延伸第一个大等于自己的数”很明显可以用单调栈，区间最小值可以用ST表，所以是线性的。

---

P1099 选数字

题意

给定长度为 \(N\) 的非负整数序列，你可以选择其中若干数，但不能有大于 \(M\) 个连续数字被选择，求所选的和最大值。\(M \le N \le 10^6\)。

解法

记 \(f_i\) 为考虑到第 \(i\) 个数字的答案且第 \(i\) 个数字必须选，我们只要考虑最长能选多长，则

$$f_i=\max_{i-m+1 \le j \le i}\{f_{j-2} + sum_{i}-sum_{j-1}\}$$

当然这个转移方程并不完全，因为选满后不一定要从 \(f_{i-m-1}\) 转移过来，故：

$$f_i=\max_{2 \le j \le i-m}\{f_{j-2} + sum_{i}-sum_{i-m}\}$$

对于两个方程我们显然是不好做的，注意有一个常用的想法：如果你设计的状态有“第 \(i\) 个必须选” 这样的性质，那可以考虑取前驱max。

所以我们状态可以改成：记 \(f_i\) 为考虑到第 \(i\) 个数字的答案。转移方程就变简单了：

$$f_i=\max\{f_{i-1},\max_{i-m+1 \le j \le i}\{f_{j-2} + sum_{i}-sum_{j-1}\}\}$$

这种方程都有个特点：从一段区间的min/max转移过来，区间的下界单调增加，并且 \(i, j\) 非常好分离，姑且称作线性min/max递推方程。这种递推dp用可以采用单调队列优化，复杂度 \(O(n)\)。

此外这题也可以反着做（所谓正难则反），最后也需要单调队列优化~

---

P1100 投资大师

题意

共有 \(T\) 天，给出每天的股票买入价 \(AP_i\)、卖出价 \(BP_i\)以及每天至多购买数量\(AS_i\)、每天至多卖出数量 \(BS_i\)。此外如果在某天进行了买入/卖出操作后，接下来的 \(W\) 天都不能再交易，且规定任何时刻持股上限为 \(MaxP\)。求最多能赚多少钱？

\(W \le T \le 2000,\ MaxP \le 2000\)。

解法

看起来有点背包的感觉，而且持股量和天数都是 \(n^2\) 级别的，因此我们记状态 \(f(i,j)\) 表示考虑到第 i 天，持股量为 j 的最大收益。（这里取了前缀max，不要求第 i 天必须交易）

则有转移：

1. \(f(i,j)=f(i-1,j)\)，即第 i 天不进行交易操作
2. \(f(i,j)=f(i-W-1,j-k)+AP_ik\)，即第 i 天买入 k 张股票
3. \(f(i,j)=f(i-W-1,j+k)+BP_ik\)，即第 i 天卖出 k 张股票

这样转移是 \(O(n^3)\) 的，但是我们发现这也是滑动区间的max问题，所以可以上单调队列优化就能变成 \(O(n^2)\)。

---

P1101 特别行动队

题意

有一列长度为 \(N\) 的正整数序列 \(\{a_i\}\)，并给定一二次函数 \(g(x)=ax^2+bx+c\)，先需要你将此序列划分为若干连续段 \(\{A_k\}\)，使得

$$\sum_{i=1}^k g(\sum_{a_j \in A_i} a_j)$$

最大，\(N \le 10^6\)。

解法

仿照上面的思想，还是先想dp怎么转移。设 \(f_i\) 为第 i 个位置一定是断点的最大值，则有：（这里这么设计一是转移简单，二是第 n 个位置一定是断点）

$$f_i=\max_{1 \le j < i}\{f_j+g(sum_i-sum_{j})\}$$

我们发现这有点类似上一题的转移了，但是这时候后面那一项不再是线性的了（关键在于有一项关于 i 的和一项关于 j 的乘在一起了），单调队列已经无能为力。

这种问题一般可以抽象成形如以下的式子：

$$b_i={\min or \max}_{j \in window} \{y_j-k_ix_j\} $$

可以用斜率优化进行处理，用单调队列维护一个凸包，复杂度 \(O(N)\)。

---

后记

第一次数据结构小作业主要设计树状数组、线段树和平衡树，都是 log 高效数据结构。

前两个我认为优化之处都在于维护了尽量少的一组“基信息 (\(N \log N\) 规模) ”使得对于任意的区间都能通过至多 log 个基组合出来。平衡树则比较多样了，比如Splay它是通过旋转不改变树性质（树性质是查找快速的关键）却能改变树高，进而使得树尽量平衡。

第二次小作业主要集中于单调栈、单调队列以及它们在优化dp方面的应用。这两个数据结构都十分“残忍”：如果一个数据比另一个数据全方位“有用”，那么没用的数据就会被丢掉。一般来说它们考虑到两个维度：值的大小、时序的先后。如果值和时序都不占优，就会有被丢掉的风险。

什么时候会用到这两个呢？首先这两个复杂度都是线性，可以对数据范围猜一猜；其次单调栈一般很好处理“离当前最近的比它大的”，或是“向左最长的以它为最大值”这类问题；而单调队列本质就是滑窗，一进一出，具体的dp式出来后就比较明显。如果有i和j乘起来的部分就得考虑斜率优化了。